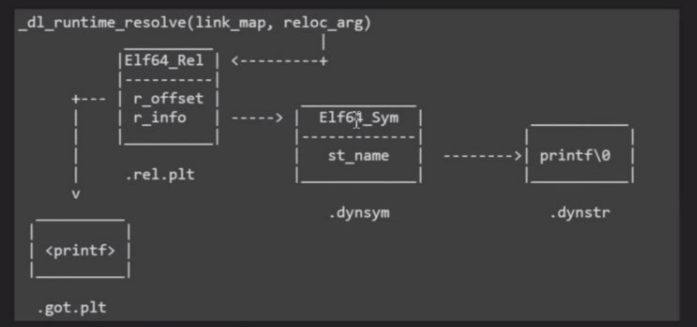
挺多地方都会应用这个知识点的,像PWN里的GOT劫持啊,ret2dl_resolve啊,Hook里的GOT Hook啊之类的
这里为了可以获得带有调试信息的libc,下载对应版本libc:http://mirrors.ustc.edu.cn/gnu/libc/ 然后开始编译
64位:
1 | cd glibc && mkdir build && cd build |
32位:
1 | cd glibc && mkdir build32 && cd build32 |
好了,那么先来说说什么是延迟绑定技术
呐,这个呢就得从动态链接说起,因为呢为了提高这一过程的效率,将符号链接这一过程呢放在了运行时,也就是当你调用的某个函数的时候呢,再去链接,为什么这样做呢?因为大部分库函数可能你并不会用到,如果提前链接这么多函数,效率肯定很低,那么第一次运行时再去绑定函数地址,然后后面再次调用这个函数时则不需要重复链接了,可以直接调用,这样做能够相对提高不少效率
先来看一个简单的程序:
1 | # include<stdio.h> |
然后指定glibc版本编译,这里引用的是我编译好的glibc存放的目录
1 | hello.o: hello.c |
然后再在命令行下指定下LD_LIBRARY_PATH路径(这只是临时的,退出这个shell即失效)
1 | export LD_LIBRARY_PATH=/home/ubuntu/debugGlibc/lib |
然后查看一下链接情况
ldd hello 1 ↵
linux-vdso.so.1 => (0x00007ffe2ce89000)
libc.so.6 => /home/ubuntu/debugGlibc/lib/libc.so.6 (0x00007f95a4abd000)
/home/ubuntu/debugGlibc/lib/ld-2.23.so => /lib64/ld-linux-x86-64.so.2 (0x0000562803699000)
然后用gdb挂上开始跟进源码调试,来看一看内部到底是怎样实现延迟绑定的
执行到这一步
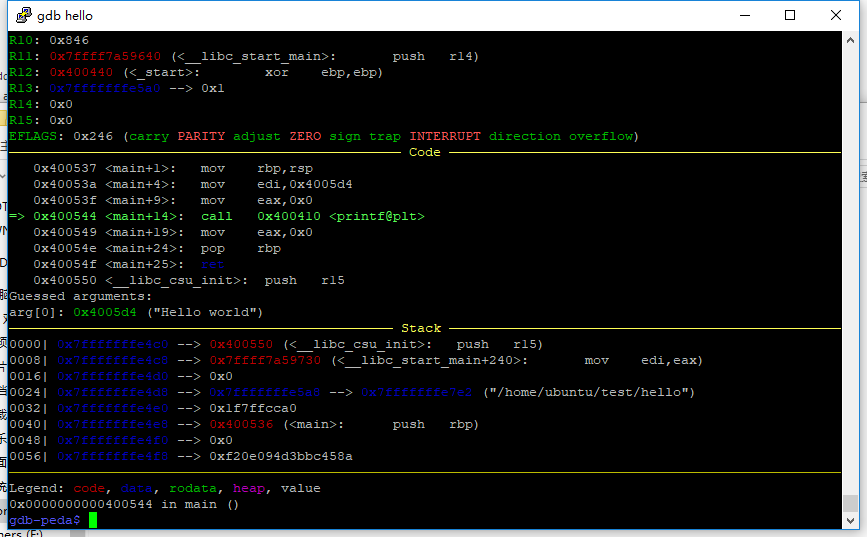
跟进去看一哈,发现进行了一个跳转
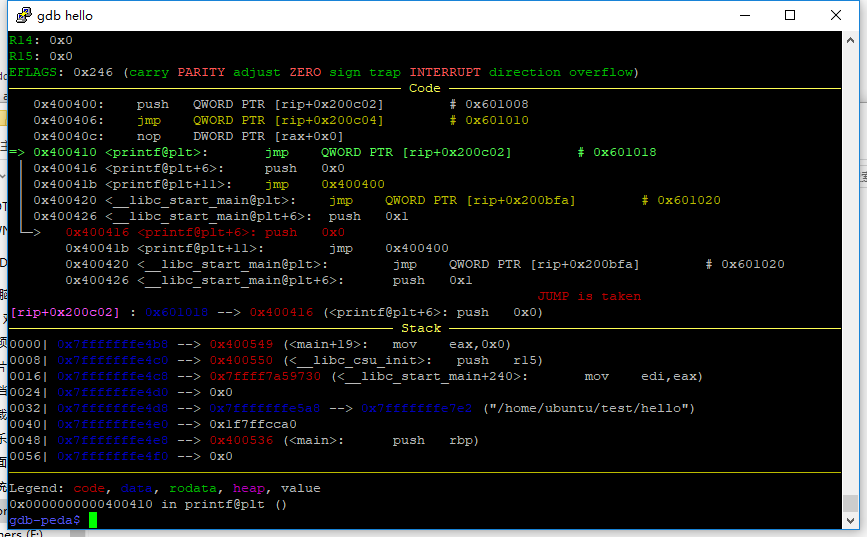
转到那个跳转处,可以发现跳转处又再次指向了printf的PLT处
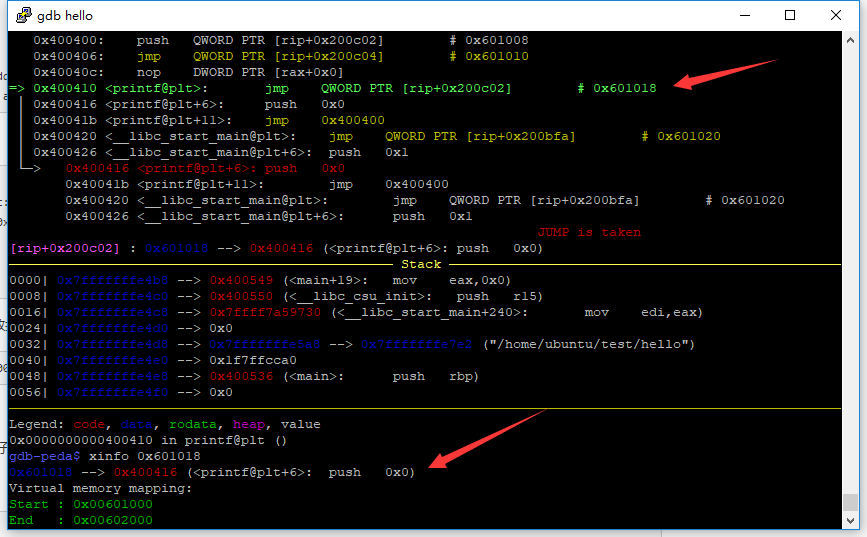
那么继续执行,此处传入了一个参数后又继续跳转
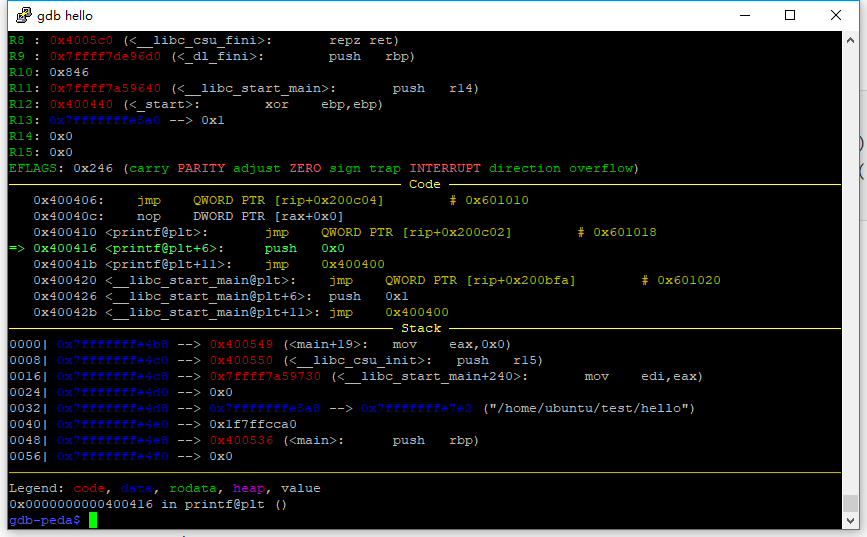
此处传入的参数其实是一个Elf64_rela结构体索引参数reloc_arg
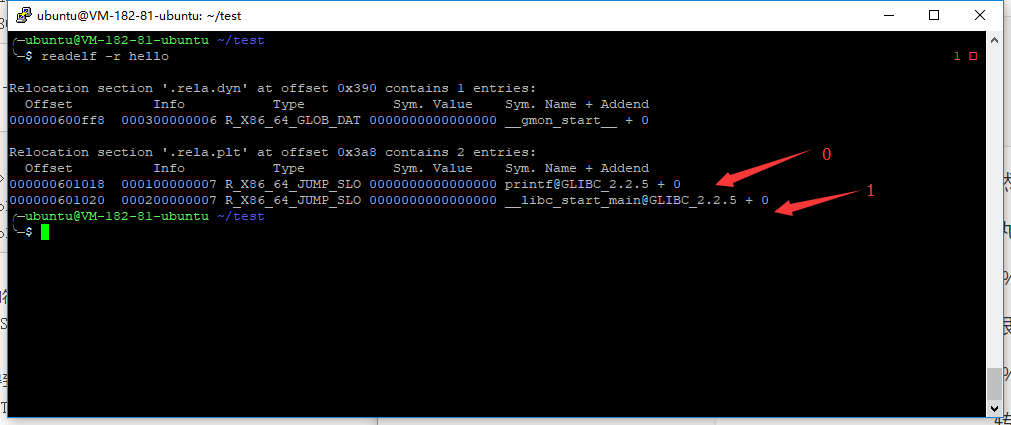
我们查看一下这两个结构体
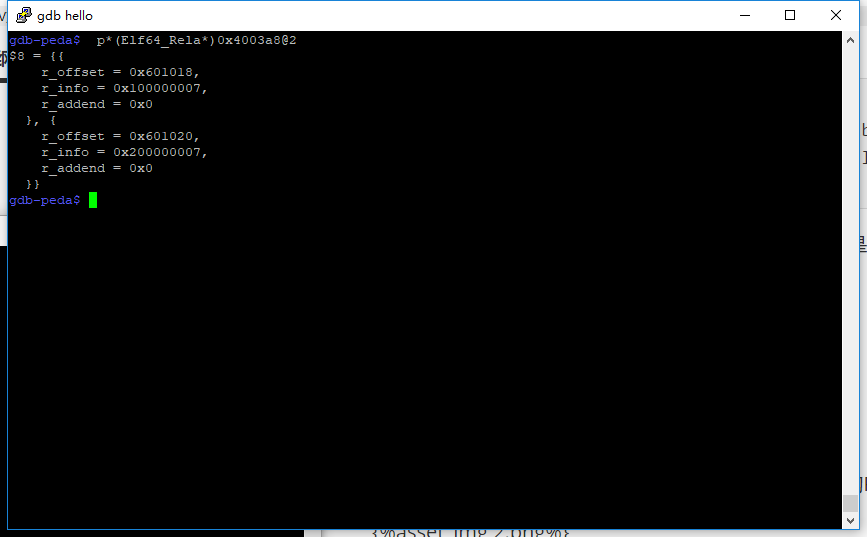 ,可以发现和我们之前有readelf工具查看的一致,那么这个结构体有两个重要的变量
,可以发现和我们之前有readelf工具查看的一致,那么这个结构体有两个重要的变量- r_offset是待会符号解析完需要回填的地址
- r_info是在.dynsym中的偏移
可以先试着手动解析一下符号,先查看一下symtab和strtab,前者包含了链接时的符号信息,后者包含了所有字符串,先跟过去看下
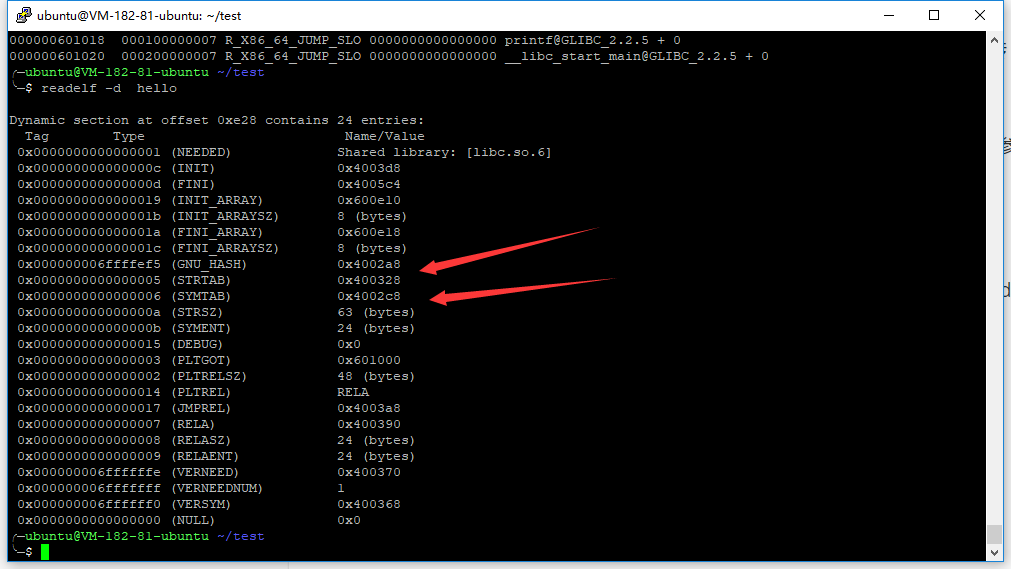
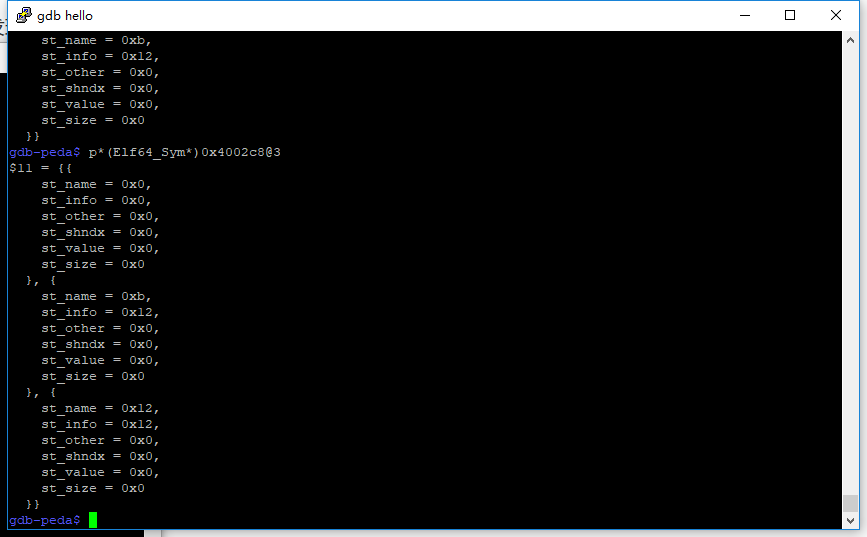
根据r_info可以得到对应的Elf64_Sym结构体,然后找到st_name,再根据这个就能去strtab索引到符号了
那么对着来,先看索引1
st_name = 0xb,然后去strtab找
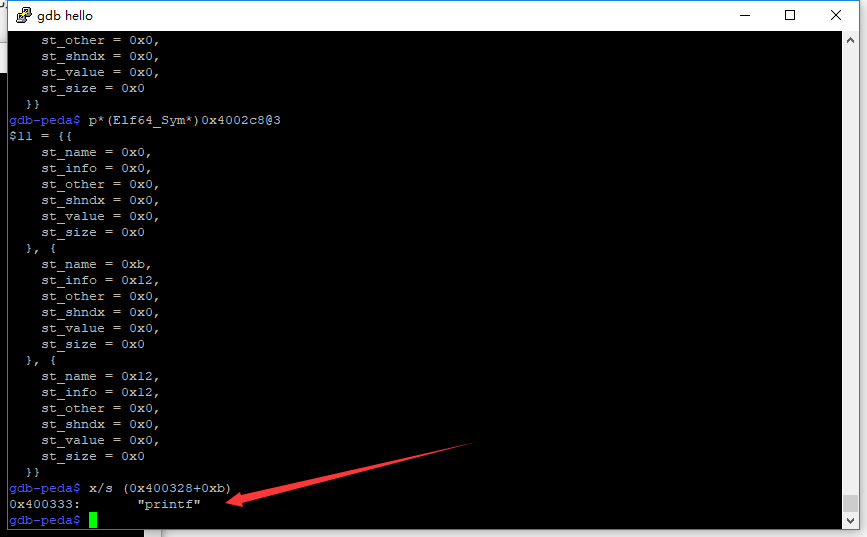
再看哈第二个
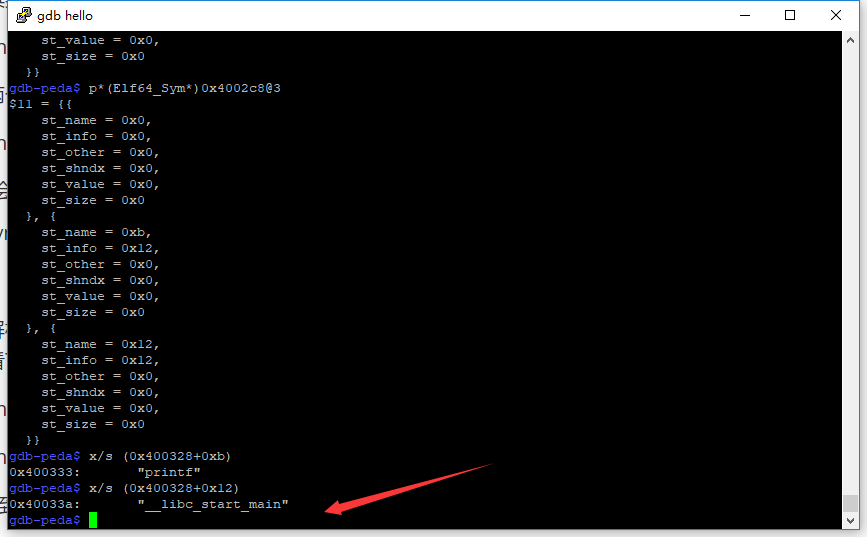
和之前分析的完全吻合!那么,这样就手动解析了一下符号信息,那么系统是怎样调研的呢,继续刚才的地方跟进
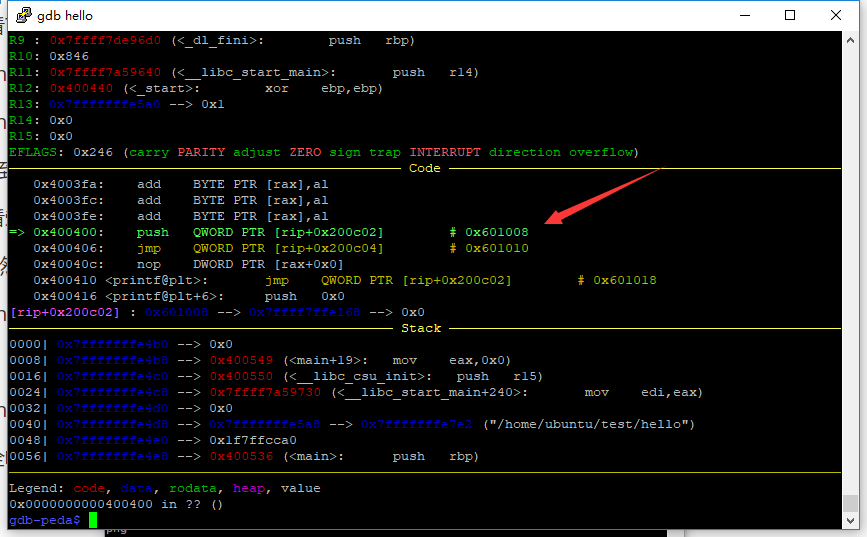
此处传入的其实是一个linkmap的指针(也有的资料 把linkmap叫做GOT[1])
指向已经加载的共享库的链表地址,然后我们跳到dl_runtime_resolve去执行(有的资料叫做GOT[2])
那么之前的步骤其实就是为了执行_dl_runtime_resolve(link_map, rel_offset);
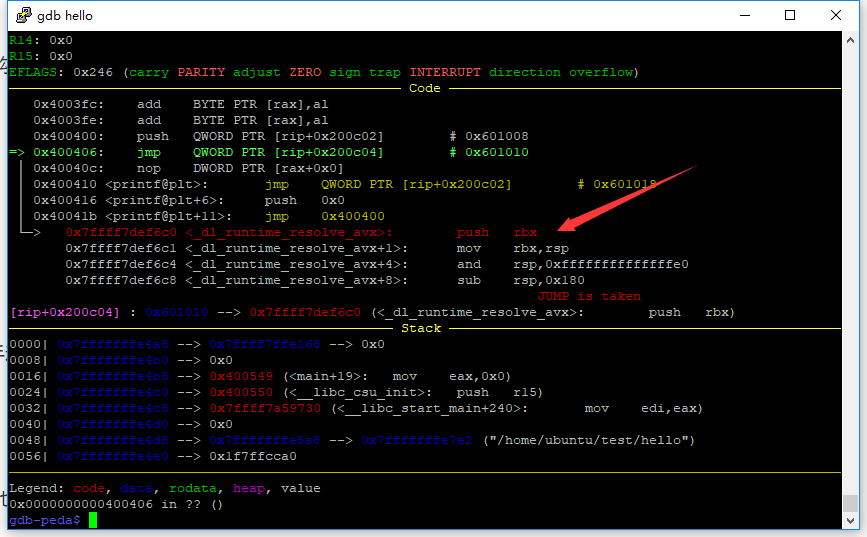
来分析下这个函数的源码,一直跟进,可以发现会跳到一个dl_fixup函数里执行
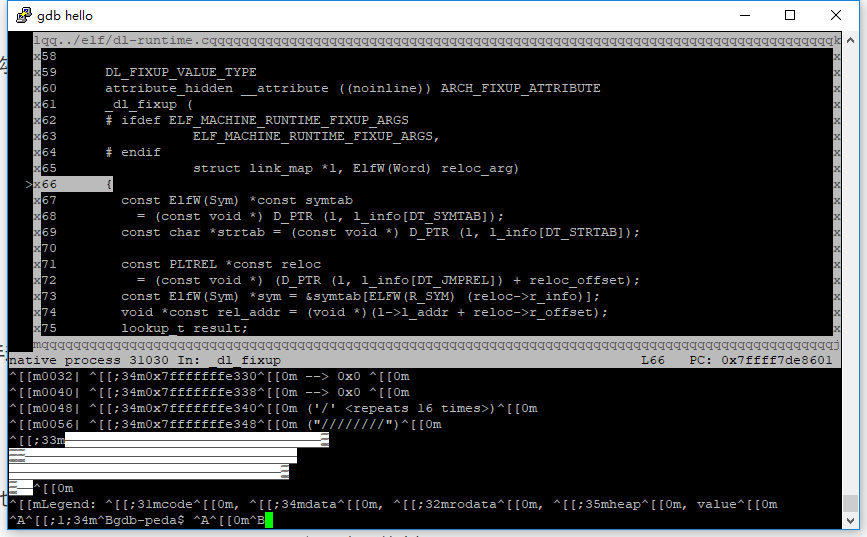
扫一下源码,最后返回值为这个
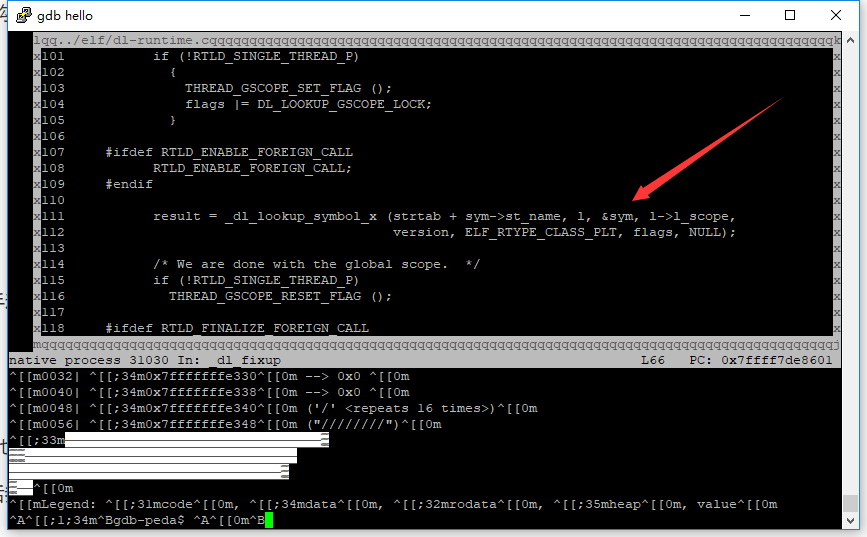
可以发现和之前手动解析的计算方式一致,然后根据解析后的符号获取对应的函数,再将函数地址进行回填,下次再调用时,就直接跳转到函数处执行
这里有张图可以帮助理解整个过程